Strange attractors are capable of generating amazingly diverse shapes from abstract to concrete, and to butterflies - see more here. However, all these images are single realizations of specific parameters and initial conditions. And they are static, so I wondered: is it possible to add some movements, some dynamic to strange attractors?

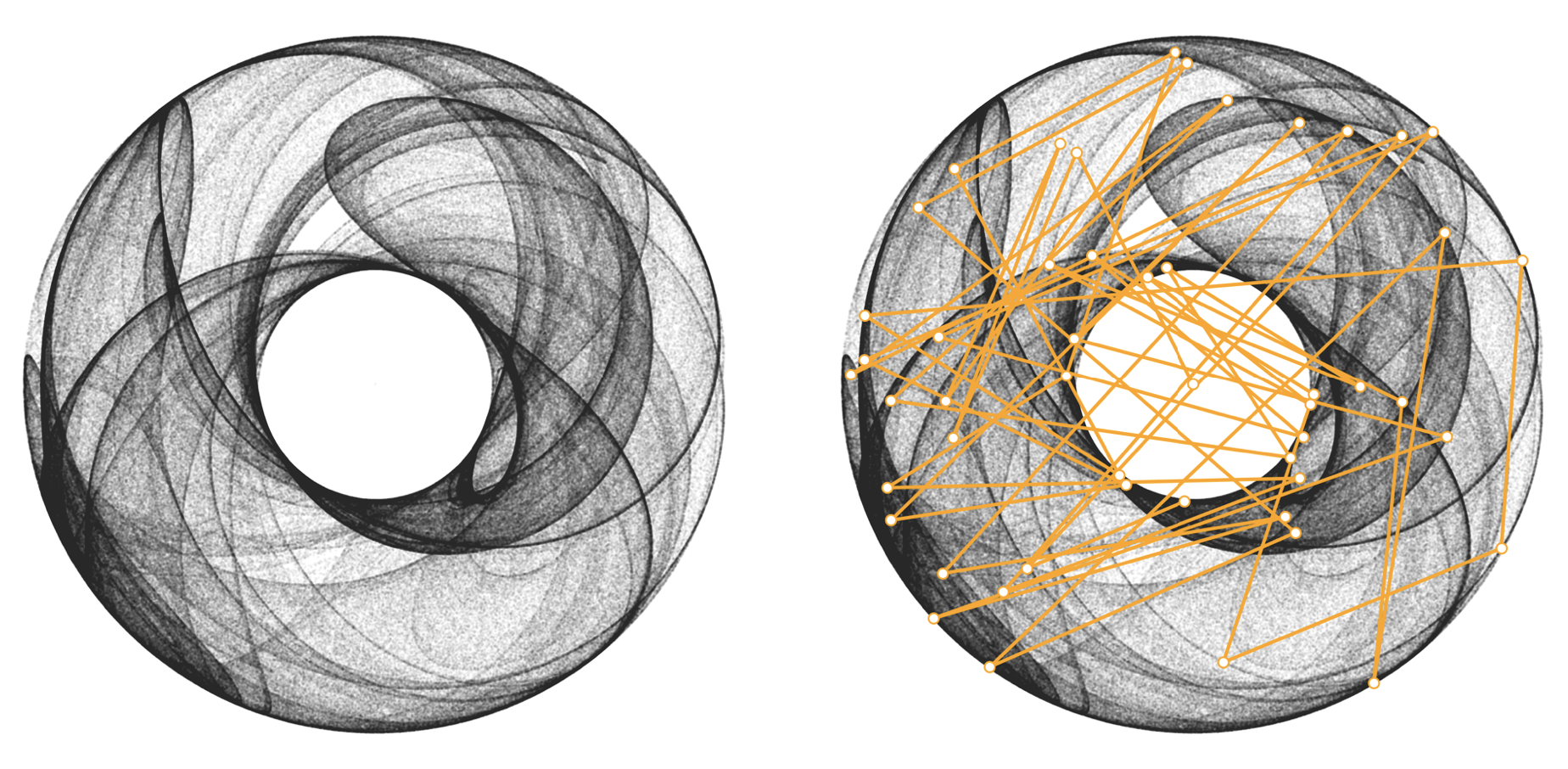
“Strange” attractors are called strange because they tend to behave in strange, chaotic ways. Some chaotic attractors like the Rössler and Lorentz have quite fluid dynamics, and its possible to get smooth movements of particles that move on the attractors. Other attractors, like the Clifford, have very chaotic maps, and plotting the movement of particles on them often results in a big tangle, or messy hairball (see below). Adding movement to such systems can be difficult as the attractors do not necessary have a temporal dimensions.

I’ve used a different approach. Cheating slightly, I instead perturb the parameters with minuscule values, which if done over and over again generate the effect of “time” and results in changing shapes. We can then capture these shapes and stick them together into a animation.

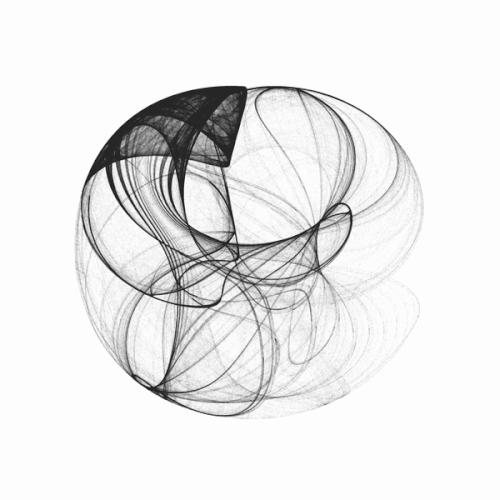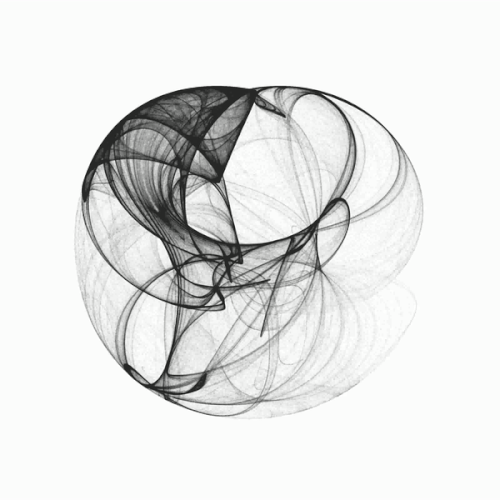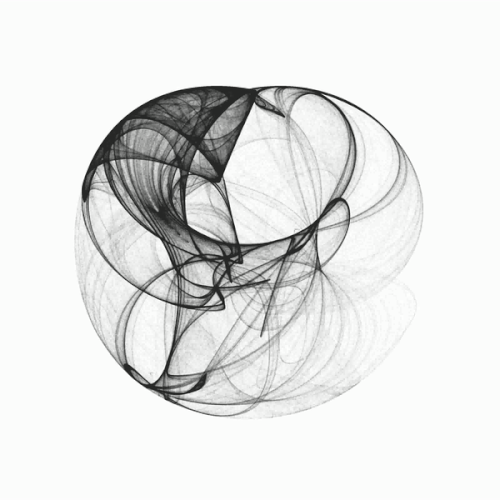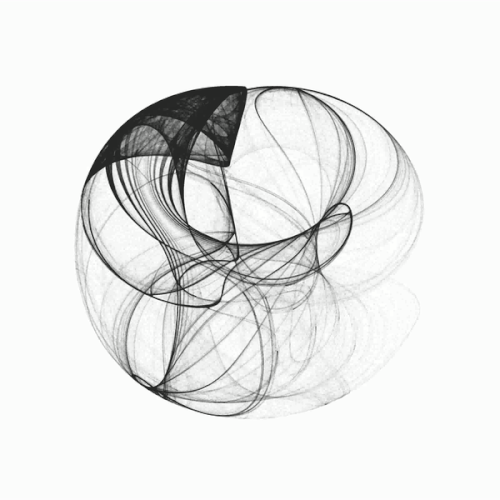
Multiple dimensions of change

I think the above animation is pretty cool, but it only shows what happens if we change one parameter, but the Clifford attractor has 4 parameters. In the equation system below it is possible to change the \(a\), \(b\), \(c\), and \(d\) parameters.

So lets change the parameters, however, to see the influence of each parameter we keep the others fixed and crate 4 separate animations, which we then glue together into one. Also, lets add some color. the below gif shows what happens when the \(a\) (top left), \(b\) (top right), \(c\) (bottom left), and \(d\) (bottom right) parameters are varied. I love playing around with chaotic systems as the always produce great visualizations.